culcameten1981.netlify.com

After finding the number of ways to get four-of-a-kind for four cards in a poker hand, should you use: a. 48 choose 1 or b. 12 choose 1 x 4 choose 1. Much of this section is based on an article by Snell and Vanderbei.18. One must be very careful in dealing with problems involving conditional probability. The reader will recall that in the Monty Hall problem (Example 4.6), if the contestant chooses the door with the car behind it, then Monty has a choice of doors to open. COMBINATORIAL PROBABILITY: POKER HANDS We have the table of probabilities for poker hands as follows: recall that the ‘scoring’ cards are denoted x and y, the other cards are denoted a, b etc.

Poker Hand Probability Problems Solving

Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?

Poker Hand Probability Problems Worksheets

The Probability of drawing a given hand is calculated by dividing the number of ways of drawing the hand (Frequency) by the total number of 5-card hands (the sample space; =, ). For example, there are 4 different ways to draw a royal flush (one for each suit), so the probability is 4 / 2,598,960, or one in 649,740. The probability of collecting royal flush in poker is 1 to 649 740. The odd to catch this combination on the flop with pocket broadway cards is equal to 0.0008%. If there is a potential royal flush on the board, the probability that it will be collected on the turn is 2%, and till the river – 4%.

Find the probability of getting the following hands in a game of traditional 5 card poker.

(1)) P(Having exactly 2 Aces) (other 3 cards can be anything but aces)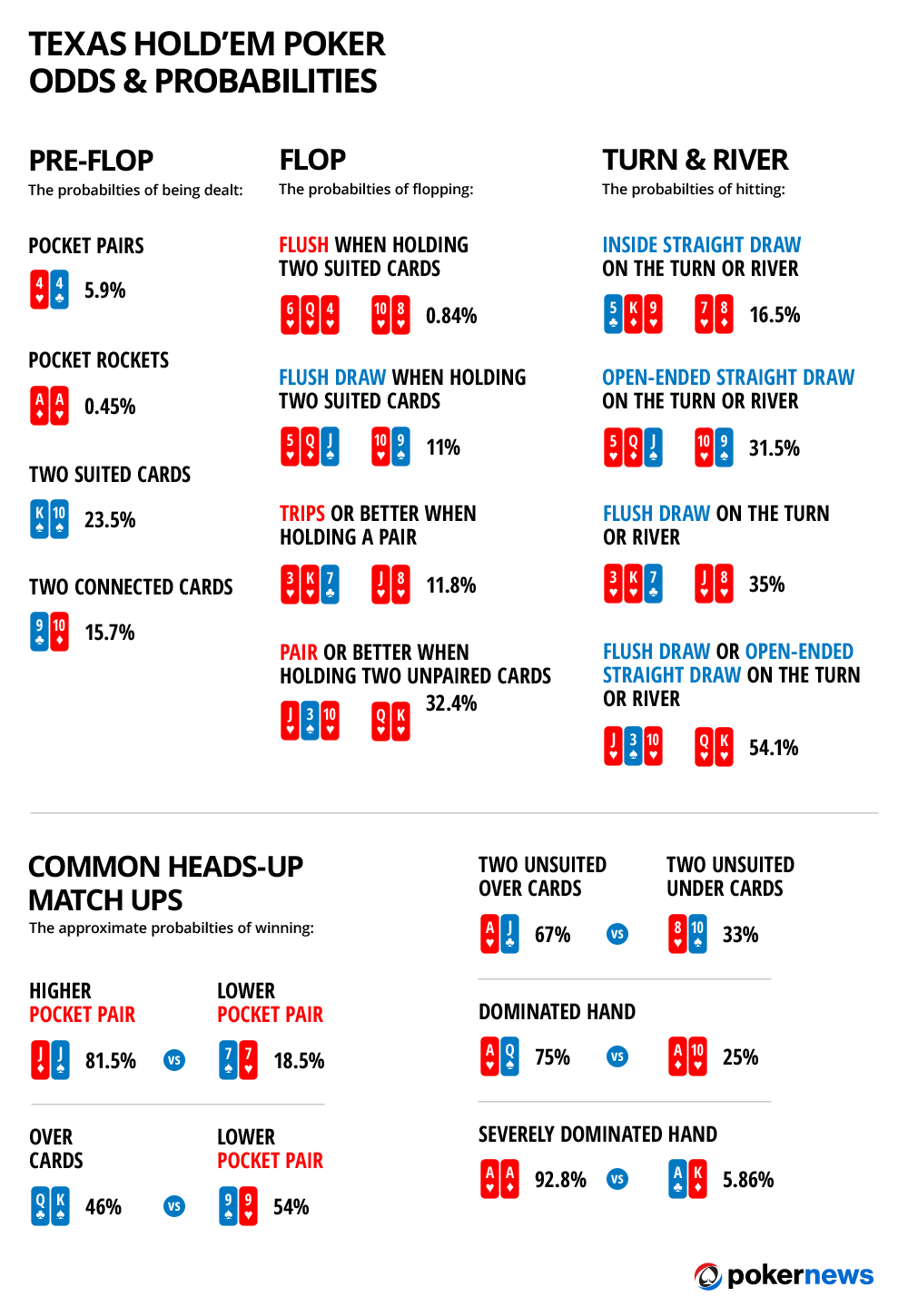

(2)) P(Royal Flush) (aka 10, J, Q, K, A and all the same suit)(3)) P(Straight Flush) (aka same suit, in consecutive number order)(4)) P(Flush) (aka all cards in the same suit.)(5)) P(Straight) (aka all cards in consecutive number order.)

Poker Hand Probability Problems

(6)) P(Full house) (aka 3 of a kind and a pair)(7)) P(Four of a kind)(8)) P(Three of a kind)(9)) P(Two pair)(10)) P(One Pair)(11)) P(No pair)

See Related Pages()

(bullettext{ Probability with Coin Tosses})
(,text{Prob(3 heads)}=frac{1}{8})

(bullettext{ Probability with Marbles })
(,text{Prob(3 red)}=frac{7}{20}…)

(bullettext{ Probability with Dice})
(,text{Prob(Two 6’s)}=frac{1}{36}…)

(bullettext{ Probability with Round Tables})
(,(n-1)!…)

(bullettext{ Probability with Poker Hands})
(,text{P(Full House)}=…)

Search More Math Topics

Poker Hand Probability Problems Worksheet

Poker Hand Probability Problems Involving

(bullettext{ Andymath Homepage})

Please Subscribe on Youtube